IMPORTANCE OF INFERENTIAL STATISTICS
There are some statistical concepts that need to be understood to understand the function of different inferential statistics. Here are the blog posts that serve as the foundations to help us understand the reason we can accept or disapprove of a phenomenon.
Concepts like Standard Error and Central Limit Theorem help us realize that we are not in a position to attempt to draw inferences about the population of a sample. Z scores, as well as Probability Distribution, assist us in understanding the different probabilities that come with normal distribution. A brief overview of the t-tests can help us understand how to determine probabilities in the event the distribution isn’t normal. Hypothesis testing explains what hypothesis testing is and what it means by accepting or rejecting it.
The terms discussed in the following posts are utilized in all types of inferential statistics. This can aid us in understanding the output that various statistical models generate.
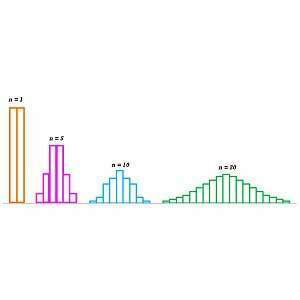
Standard Error of Mean and Central Limit Theorem
In the present blog, some concepts are covered, including standard error, which is an indication of the accuracy of statistics, Standard Error of Mean, which is utilized in formulas used in various inferential statistics as well as the Central Limit Theorem, which is the foundational principle of Inferential Statistics.

Z scores, Z test, and Probability Distribution
Methods for measuring Variability are used here as examples of how variance can be utilized to draw conclusions about the data of the population. The notions in Measures of Shape also come into play to look at how probabilities are drawn from how the distribution is shaped.

A brief intro to T Test
An introduction to what a t-test is, how it is built on t distribution, and why it's crucial. Questions like how it differs in comparison to Z Test are also discussed in this article.

Hypothesis Testing
Concepts such as what hypotheses testing involves, and what is the meaning of p-value or confidence level, significance level, types I and II error null hypothesis, and one-tailed and two-tailed hypothesis are discussed in this blog post.
