Overview
T-Tests are a form of hypothesis tests. A brief introduction to T-Tests explains them. T-Tests can be used when two means are compared and need to be determined if they are statistically distinct from one another. T-Tests use the T distribution family and the T table to calculate the p-value. T-Tests can be used when the sample size of the population or standard deviation is unknown, as explained in previous blogs on T-Tests.
There are three main types of T-tests.
- One-Sample T-Test
- Paired two samples of T-Test (Dependent Test-Test).
- Independent two-sample T-Test (Independent T-Test)
One-Sample T-Test
One sample T-Test, the most basic of all T-Tests, is also the most important. It can be used to explain the T-Tests. One-Sample Test is used to determine if the sample mean is equal to or significantly different from the population mean. When we need to compare one sample means to a null hypothesis. This T-Test requires one continuous (interval scaled) independent variable and one categorical dependent variable. The T-Test is similar to other hypothesis tests. First, a value must be found. This will be the T value. The p-value can be determined by reviewing the T Table based on the T value and degrees of freedom. The T Table can be used to determine whether the Null Hypothesis should be rejected. The Null Hypothesis states that there is no difference in the Sample Mean and Null Hypothesis values (e.g., The population means, i.e., H0: u1 = x1. The hypothesis is that these two values are statistically significantly different from one another, i.e., HA: u1 x1. This assumes that the variables are roughly normally distributed.
Understanding how One sample T-test works is crucial. Here is the formula for the T value.

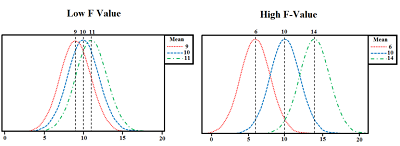
The easiest and most popular way to understand the T-Test’s formula is to use the analogy T value is like the signal/noise ratio, where the numerator represents the signal, and the denominator represents the noise.
The numerator, which is the result of subtracting the Null Hypothesis value from the sample means, can be considered the Signal of Signal-to-noise. The ratio will increase as the difference between the null hypothesis and sample values increases (in either direction). The output can either be negative or positive. If the signal strength is low, the output will increase.
The formula for the t value’s denominator is the standard error of means. As discussed in the blog post, standard error, standard error of median and central limit theorem, and standard error of mean show how close our sample mean to the population’s mean. A higher value denominator indicates a more random error. The denominator here is analogous to Noise. This is because the difference between the null hypothesis and sample means increases. Therefore, the fraction is used to determine whether the signal is significant enough.
The signal-to-noise ratio (T Value) measures how distinct the signal is from the noise. If the signal is too small or too loud, causing it not to stand out, then the null hypothesis must be considered. After considering the significance level and p-value, the null hypothesis should be considered. The difference in population and sample mean can be attributed to random chance.
Degrees of Freedom must also be taken into consideration. You can calculate the degrees of freedom by subtracting 1 from N (numbers of samples). Once the t value, degrees of freedom, and T table are available, you can use the T table to determine the p-value to accept or reject the null hypothesis.
Paired two samples T-Tests (Dependent Test-Test)
One-Sample and Paired Two Sample T-Tests are nearly the same things. This is unlike One-Sample Test, where the sample means and the Null Hypothesis value are compared. Here, two means from a single sample or two matched/paired samples can be compared (e.g., before/after). The levels of the variable can also be attributed back to the time (before or after), which is similar to Repeated Measures ANOVA. However, the assumptions for normality in each of these tests are slightly different. Paired dependent T-Test requires that the continuous variable be approximately normal, while Repeated measure ANOVA requires that every level (or group) of the continuous variables be normal.
Paired Two and One Sample work in the same way. The paired sample T-test simply calculates the difference between the paired observations (e.g., before and after), and then a 1-sample-t-test is done.
While the paired t-test has its advantages, it can also work when the assumption of normality fails. However, the distribution must be continuous, unimodal (having just one mode), and symmetric. Non-parametric methods are used if the distribution is not at least approximately normal.
It is easy to determine whether one sample T-Test or another T-Test should be used. This is done by comparing the scores of each row in the dataset to see if they are the same subject. A row in a dataset represents marks for student ‘A’ prior to academic coaching and after coaching. Paired two-sample tests can be used if the subject is the same. If the differences in the values are not related to the same subject, an independent two-sample test can be used.
An example of Dependent t Testing can be: Is there a difference in the average marks achieved by a group of students on a standardized exam? They took two exams: one at the beginning and one at the end.
In this scenario, the formula to calculate the t value for Paired Two Sample T-Test is-
or

The difference (between student scores) can sometimes be positive, negative, or null. These values will come from their own distribution with a mean and standard deviation, and this standard error will be the difference between the samples. This standard deviation is used in the faction to calculate the t value. This formula is a two-step process to calculate the standard error of the difference between the dependent sample’s means.
where,
S Dis a standard error for the difference between dependent samples means
S D is the standard deviation of the difference among dependent sample means
D is the difference between each pair’s X and Y scores. (i.e., X -Y).
N is the number pair of scores.
After the t value has been calculated, degrees of freedom are required to determine the p-value. The degree of freedom for Paired Two Sample T-Test can also be found by subtracting 1 from each pair of scores (marks).
Independent Two-Sample T-Test
Independent Two-Sample t-Test is generally used to compare the means of two independent samples. It is very similar to a one-sample T-Test. However, in order to conduct such a T-Test, separate groups are needed for each sample. Also, we require one categorical (nominal) independent variable, which has two levels (subcategories/groups) and one continuous (interval scaled) dependent variable. A good example of this problem is to determine if the heights of men and women differ from one another. The two-sample T-Test is used to determine if the means of the two samples are statistically significantly different from each other. If the difference is significant enough to allow us to draw inferences about the population they represent, or if it is due to random sampling. The result could be different in one sample or reversed in another. The standard error can be determined by using the analogy (signal/noise ratio) to understand the formula that calculates the t value of the Independent Two-Sample T-Test. The formula for calculating the T value is:
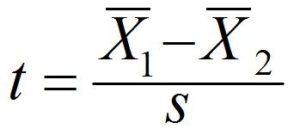
The numerator (signal) is the difference in the means of both samples. The standard error is the denominator (noise). The standard error here, in contrast to the one from the One-Sample T-Test, is not the mean error in sampling; it is simply the average error for differences Between Independent Sample Means, and it is required to add standard deviations from both samples. It isn’t that easy. We can assume equal or different levels of variability for each
group. Suppose the variance in each sample equals, and the sample sizes of both means are the same or approximately equal. In that case, the output is the Standard Error (denominator for the T value formula). The formula must be modified or adjusted if the sample sizes are different. Because we assume that all samples have the same variance and assign equal weights to them, little variance can lead to a large standard error if they aren’t ‘almost equal. These issues can be countered by non-parametric methods that use a different formula. If the sample sizes of both samples are equal, the standard error can still be calculated by adding the two standard deviations.

The T value can be used to determine the p-value. However, we must first find the degrees of freedom. In this T-Test, we take the sum of two samples and subtract two. df = N1+N2 – 2. (N1 = sample of sample 1 and N2 = sample of sample 2, respectively) As the distribution of t changes, so does the probability. We use the degrees of freedom, which are a function of the sample size.
The null hypothesis here is that there is no difference in the variability between the two groups, while the alternative hypothesis says otherwise. The signal-to-noise principle applies here. If the signal is strong, then the null hypothesis can be rejected. We must determine the significance level to get a precise result. We refer to the T-Test Table to find the p-value for the respective t-values and degrees of freedom. We can reject the null hypothesis if the p-value is lower than the predetermined significance levels. The two means of the sample are statistically significantly different.
These three types of T-Test are important in inferential statistics. They can be used when there isn’t a sufficient sample size, or the standard deviation is missing. This is why they are so popular.




