Overview
The issue is when we don’t have a population sufficient to ensure to ensure that the central limit theorem can be used or only the average for the entire population exists, but there is no standard deviation. In this case, we’ll have to calculate how much the sample’s standard deviation differs based on what we know about the average deviation in our sample. So, in such situations, the Z-test Z score, Z Table and Z Table will all become unusable. This is where the T-Test, also known as Student’s T-Test, comes into play; that has its own formula for calculating the T score that is identical to the z score/value. It also has a T-Table, which functions similar to a Z Table only with an additional column for Degrees of Freedom, which is currently, for the sake of convenience, can be explained as a number of samples minus one (N-1). By using The Score as well as the T Table, it is possible to conduct a variety of T-Tests as explained in depth within the blogs T-Tests.
In the last several blog articles, we discussed how probabilities could be determined by using an area-under-the curve using the aid of the z-value. The fundamental concept, which is the basis of this case, is that the distribution has to be normal because, in the case of normal distribution, we can be sure about the space that each individual point covers within the distribution. Let’s take a large number of different samples. It is possible to employ the Central Limit theorem, which states that if the size of the sample is sufficient (more than thirty), the sample will be able to follow an average distribution. In all of these instances, the normal variation for the sample is apparent to us. To determine the area of the curve (or probability), we use the Standard Normal Distribution Table or the z-score table as well as the z-score to determine the probabilities associated with the normal distribution.
T-Distribution
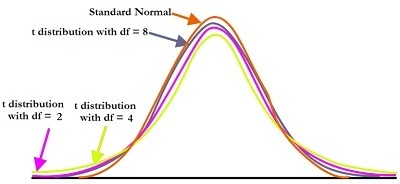
The Z test applies to Normal Distributions with specific characteristics, while the T-Test can be used on a T-Distribution with certain features. We must first know the characteristics of T-Distribution as well as the reason for it. The T Distribution is virtually identical to the normal distribution; however, as the sample size shrinks, the T Distribution becomes more rounded in the middle and more pronounced at the edges. We utilize the degree of freedom listed in this table in order to determine probabilities. The sample size is considered, i.e., degrees of freedom when there is a reduction in the size of the sample, the probability that it is associated with alters. When the sample size shrinks, the distribution begins to diverge from its normal distribution. The t-distribution can be used since it basically follows the Normal Distribution but with some required modifications.
Know More About T – Test, Visit : Introduction to T-Test: Types, Formula, Approachs
The formula used to determine T Score
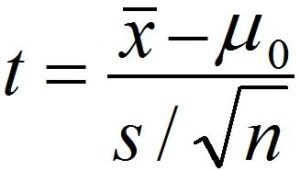
The formula to calculate the t-score can be compared to the Z-score, with the only difference being in the denominator. Instead of standard deviation, we employ the Standard Error or Mean (where you divide your sample’s standard deviation (standard error) by its square root, which is the sum of all samples).
The difference between Z and T-score
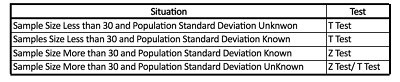
What score should be used to calculate? This is a matter which can be complicated.
There are two approaches to solving this issue. First, if your sample is smaller than 30, then only T-tests are required; however, in the case that your sample is lower than 30 and the standard variation of the sample isn’t established, then conducting a t-Test is the proper thing to do. In the event that the number of samples is larger than 30 and the standard deviation for the entire population has been determined, then Z-scores are to be calculated (i.e., Z-Test must be conducted). Suppose the sample size is sufficiently large and the standard deviation is unknown. In that case, either one of these tests may be performed since as the size of the sample increases, the variance in probabilities calculated by both tests decreases.




